Визуальные иллюзии
- Автор темы Monah
- Дата начала
Бес в ребро
Пользователь
А у меня крутяцца.
F
Frodo
Guest
Не просто внимательна аросто сканер какой то
Не знаю конечно насколько это относится к исскуству, но решила разместить здесь.)
Невозможные фигуры - особый вид объектов в изобразительном искусстве. Как правило их называют так, потому что они не могут существовать в реальном мире.
Или невозможными фигурами называют геометрические объекты, нарисованные на бумаге, которые прозводят впечатление обычной проекции трехмерного объекта, однако, при внимательном рассмотрении становятся видны противоречия в соединениях элементов фигуры.
Невозможные конструкции известны с давних времен. Они встречаются в иконах со средних веков.
К примеру на миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована Мадонна с младенцем. На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект сюрреалистичности. Но неизвестно был ли этот прием сознательным поступком художника или же его ошибкой.
И если авторы этих работ вполне могли создать невозможные фигуры случайно, допустив ошибку при проецировании изображения объемной фигуры на плоскость, то современные художники создают их специально.
"Отцом" современных невозможных фигур считается шведский художник Оскар Реутерсвард, который нарисовал свой знаменитый невозможный треугольник, составленный из кубиков еще 1934 году.
За годы творчества он придумал и нарисовал еще несколько тысяч невозможных фигур.
Серия "Окно в полу"
Серия "Флаги стран Европы"
Известны же широкой публике невозможные фигуры стали в 50-х годах 20 века, после публикации статьи Роджера Пенроуза и Лайонела Пенроуза в Британском журнале психологии, в которой были описаны две базовые фигуры - невозможный треугольник (который также называют треугольником Пенроуза) и бесконечная лестница.
В 1954 году Роджер и Лайонел Пенроузы опубликовали в Британском журнале психологии статью о двух классических невозможных фигурах - невозможном треугольнике и бесконечной лестнице. В этой статье невозможный треугольник был представлен в его классическом виде - в виде трех соединяющихся под прямым углом балок, изображенных с эффектом перспективы.
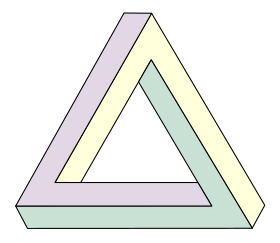В отличие от треугольника Реутерсварда, треугольник Пенроуза нарисован с использованием линейной а не параллельной перспективы, что придает ему больше невозможности.
Невозможная лестница - одна из базовых невозможных фигур. Ее еще иногда называют бесконечной лестницей.
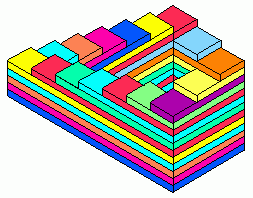Если бы кто-то захотел бы подняться или спуститься по ней, то, пройдя четыре лестничных пролета, он оказался бы в той же самой точке, откуда начал свой путь. Такую прогулку по лестнице можно продолжать до бесконечности, так и не сдвинувшись с начальной точки.
Эта статья попала в руки известного голландского художника М.К. Эшера, который вдохновленный идеей невозможных фигур создал свои знаменитые литографии "Водопад", "Восхождение и спуск" и "Бельведер".
Конструкция составлена из перекладин, положенных одна на другую под прямым углом. Следя глазами за ее элементами поочередно, мы не заметим несоответствия между ними. Однако перед нами – совершенно невозможное целое, поскольку в интерпретации расстояния между объектами и наблюдателем возникают неожиданные изменения. Эта немыслимая конструкция трижды "вмонтирована" в картину.
Прямоугольник внутреннего двора замкнут стенами здания, у которого вместо крыши – бесконечная лестница. Скорее всего, в этом дому живут монахи, приверженцы некой религиозной секты. Возможно, ежедневный ритуал предписывает им подниматься по ступеням несколько часов подряд. Кажется, если они устанут, им разрешается повернуть в обратную сторону и спускаться, вместо того чтобы подниматься. Однако оба направления, хотя и выразительны, но одинаково бесполезны.
Видео роллик с объяснением парадокса Эшера "Спускаясь и поднимаясь."
Слева на переднем плане лежит лист бумаги с чертежом куба. Места пересечения граней отмечены двумя кружками. Какая грань впереди, какая позади? В трехмерном мире невозможно увидеть переднюю и заднюю стороны одновременно, поэтому их невозможно изобразить. Однако есть возможность нарисовать предмет, передающий иную реальность, если смотреть на него сверху и снизу. Сидящий на скамье юноша держит в руках именно такое абсурдное подобие куба. Он задумчиво разглядывает этот непостижимый предмет, оставаясь безразличным к тому, что бельведер за его спиной выстроен в том же невероятном, абсурдном стиле. На полу нижней площадки, то есть внутри, стоит лестница, на которую взбираются двое. Однако, достигнув верхней площадки, они снова окажутся снаружи, под открытыми небом, и снова им придется входить внутрь бельведера.
Другие работы Эшера здесь.
Вслед за Эшером огромное количество художников по всему миру стали использовать невозможные фигуры в своем творчестве. Наиболее известны среди них Жос де Мей, Сандро дель Пре, Оштван Орос. Работы этих, а также других художников, выделяют в отдельное направление изобразительного искусства - "имп-арт", от английских слов impossible ("невозможный") и art ("искусство").
Самое интересное, что существуют определенные способы, которые позволяют воспроизвести невозможные фигуры в реальном мире, правда они будут выглядет невозможными только с одной точки обзора. С других точек обзора видны искажения и разрывы в фигуре.
Конечно, ни одну из невозможных фигур нельзя создать, действуя прямолинейно. Например, если вы возьмете три одинаковых деревянных бруска, вы не сможете совместить их так, чтобы получился невозможный треугольник. Однако, при проецировании трехмерной фигуры на плоскость некоторые линии могут становиться невидимыми, перекрывать друг друга, стыковаться друг с другом и т.п. Исходя из этого, мы можем взять три различных бруска и составить треугольник, представленный на фотографии ниже .
Данная фотография создана известным популяризатором работ М.К. Эшера, автором большого количества книг Бруно Эрнстом. На переднем плане фотографии мы видим фигуру невозможного треугольника. На заднем плане установлено зеркало, в котором отражается та же фигура с другой точки зрения. И мы видим, что на самом деле фигура невозможного треугольника является не замкнутой, а разомкнутой фигурой. И только с той точки, с которой мы обозреваем фигуру кажется, что вертикальный брусок фигуры заходит за горизонтальный брусок, вследствие чего фигура кажется невозможной. Если бы мы сместили угол обзора немного, ты нам сразу бы стал виден разрыв в фигуре, и она потеряла бы свой эффект невозможности. Тот факт, что невозможная фигура выглядит невозможной только с одной точки зрения характерен для всех невозможных фигур.
Если невозможный треугольник относительно несложно сконструировать в реальном мире, то совсем создать невозможный трезубец в трехмерном пространстве не так-то просто. Особенностью этой фигуры является наличие противоречия между передним и задним планом фигуры, когда отдельные элементы фигуры плавно преходят в фон, на котором расположена фигура.
Если закрыть рукой верхнюю часть трезубца, то мы увидим вполне реальную картину - три круглых зуба. Если закрыть нижнюю часть трезубца, то мы тоже увидим реальную картину - два прямоугольных зубца. Но, если рассматривать всю фигуру целиком, то получается что три круглых зубца постепенно превращаются в два прямоугольных.
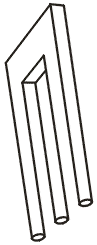Таким образом, можно увидеть, что передний и задний планы данного рисунка конфликтуют. То есть, то что было изначально на переднем плане уходит назад, а задний план (средний зуб) вылезает вперед. Кроме смены переднего и заднего планов в данном рисунке присутствует еще один эффект – плоские грани верхней части трезубца становятся круглыми в нижней.
Эффект невозможности достигается за счет того, что наш мозг анализирует контур фигуры и пытается подсчитать количество зубцов. Мозг сравнивает количество зубцов фигуры в верхней и нижней части рисунка, из-за возникает ощущение невозможности фигуры. Если количество зубцов у фигуры было значительно больше (например, 7 или 8), то это парадокс был бы менее ярко выражен.
Некоторые книги утверждают, что невозможный трезубец принадлежит к классу невозможных фигур, которые не могут быть воссозданы в реальном мире. На самом деле это не так. ВСЕ невозможные фигуры можно увидеть в реальном мире, но невозможными они будут выглядеть только с одной единственной точки зрения
В Институте Глазной Оптики в городе Аахен (Германия) смогли решить эту задачу, создав специальную установку. Конструкция состоит из двух частей. В передней части расположены три круглые колонны и строитель. Эта часть освещается только внизу. За колоннами расположено полупроницаемое (half-permeable) зеркало с отражающим слоем, расположенным спереди, то есть зритель не видит то, что находится за зеркалом, а видит в нем только отражение колонн.
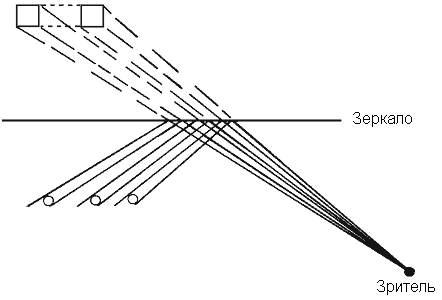Изображение в зеркале меняется, когда включаются источники света, расположенные за зеркалом. Тогда зрителю становятся видны две квадратные колонны и поперечная балка, находящиеся за зеркалом и освещаемые только в верхней части.
Вроде бы серьезные учереждения, а работают над проблемами превращения нереального в реальное, правда не безуспешно.
Большинство материала взято с сайта про невозможные фигуры здесь.
Интересно иллюзии неправильных фигур объясняют психологи.
Невозможные фигуры - особый вид объектов в изобразительном искусстве. Как правило их называют так, потому что они не могут существовать в реальном мире.
Или невозможными фигурами называют геометрические объекты, нарисованные на бумаге, которые прозводят впечатление обычной проекции трехмерного объекта, однако, при внимательном рассмотрении становятся видны противоречия в соединениях элементов фигуры.
Невозможные конструкции известны с давних времен. Они встречаются в иконах со средних веков.
К примеру на миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована Мадонна с младенцем. На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект сюрреалистичности. Но неизвестно был ли этот прием сознательным поступком художника или же его ошибкой.
Или колонны с иконы 15 века "Страшный суд"
"Отцом" современных невозможных фигур считается шведский художник Оскар Реутерсвард, который нарисовал свой знаменитый невозможный треугольник, составленный из кубиков еще 1934 году.
Серия "Окно в полу"
Серия "Флаги стран Европы"
Известны же широкой публике невозможные фигуры стали в 50-х годах 20 века, после публикации статьи Роджера Пенроуза и Лайонела Пенроуза в Британском журнале психологии, в которой были описаны две базовые фигуры - невозможный треугольник (который также называют треугольником Пенроуза) и бесконечная лестница.
В 1954 году Роджер и Лайонел Пенроузы опубликовали в Британском журнале психологии статью о двух классических невозможных фигурах - невозможном треугольнике и бесконечной лестнице. В этой статье невозможный треугольник был представлен в его классическом виде - в виде трех соединяющихся под прямым углом балок, изображенных с эффектом перспективы.
Невозможная лестница - одна из базовых невозможных фигур. Ее еще иногда называют бесконечной лестницей.
Эта статья попала в руки известного голландского художника М.К. Эшера, который вдохновленный идеей невозможных фигур создал свои знаменитые литографии "Водопад", "Восхождение и спуск" и "Бельведер".
Видео роллик с объяснением парадокса Эшера "Спускаясь и поднимаясь."
Другие работы Эшера здесь.
Вслед за Эшером огромное количество художников по всему миру стали использовать невозможные фигуры в своем творчестве. Наиболее известны среди них Жос де Мей, Сандро дель Пре, Оштван Орос. Работы этих, а также других художников, выделяют в отдельное направление изобразительного искусства - "имп-арт", от английских слов impossible ("невозможный") и art ("искусство").
Самое интересное, что существуют определенные способы, которые позволяют воспроизвести невозможные фигуры в реальном мире, правда они будут выглядет невозможными только с одной точки обзора. С других точек обзора видны искажения и разрывы в фигуре.
Конечно, ни одну из невозможных фигур нельзя создать, действуя прямолинейно. Например, если вы возьмете три одинаковых деревянных бруска, вы не сможете совместить их так, чтобы получился невозможный треугольник. Однако, при проецировании трехмерной фигуры на плоскость некоторые линии могут становиться невидимыми, перекрывать друг друга, стыковаться друг с другом и т.п. Исходя из этого, мы можем взять три различных бруска и составить треугольник, представленный на фотографии ниже .
Если невозможный треугольник относительно несложно сконструировать в реальном мире, то совсем создать невозможный трезубец в трехмерном пространстве не так-то просто. Особенностью этой фигуры является наличие противоречия между передним и задним планом фигуры, когда отдельные элементы фигуры плавно преходят в фон, на котором расположена фигура.
Если закрыть рукой верхнюю часть трезубца, то мы увидим вполне реальную картину - три круглых зуба. Если закрыть нижнюю часть трезубца, то мы тоже увидим реальную картину - два прямоугольных зубца. Но, если рассматривать всю фигуру целиком, то получается что три круглых зубца постепенно превращаются в два прямоугольных.
Эффект невозможности достигается за счет того, что наш мозг анализирует контур фигуры и пытается подсчитать количество зубцов. Мозг сравнивает количество зубцов фигуры в верхней и нижней части рисунка, из-за возникает ощущение невозможности фигуры. Если количество зубцов у фигуры было значительно больше (например, 7 или 8), то это парадокс был бы менее ярко выражен.
Некоторые книги утверждают, что невозможный трезубец принадлежит к классу невозможных фигур, которые не могут быть воссозданы в реальном мире. На самом деле это не так. ВСЕ невозможные фигуры можно увидеть в реальном мире, но невозможными они будут выглядеть только с одной единственной точки зрения
Вроде бы серьезные учереждения, а работают над проблемами превращения нереального в реальное, правда не безуспешно.
Большинство материала взято с сайта про невозможные фигуры здесь.
Интересно иллюзии неправильных фигур объясняют психологи.
Как пример на картинах Жос де Мея.
Вообще от просмотра таких картин мозги "кипят" и у меня как то слабо приспосабливаются к геометрическим противоречиям.)
[quote name=\'mariska\' post=\'413728\' date=\'3.5.2009, 19:38\']Вообще от просмотра таких картин мозги "кипят" и у меня как то слабо приспосабливаются к геометрическим противоречиям.)[/quote]
точно)) (а помнишь тема была про обман зрения что ли, и там картинку как раз выкладывали - она здесь шестая, вот тогда я еще не совсем поняла, а в чем собственно то дело и особо не впечатлилась.. теперь все яснее (слава пояснениям и более крупному изображению!
)
и хоть и кипят, но черртовски же занятно))
точно)) (а помнишь тема была про обман зрения что ли, и там картинку как раз выкладывали - она здесь шестая, вот тогда я еще не совсем поняла, а в чем собственно то дело и особо не впечатлилась.. теперь все яснее (слава пояснениям и более крупному изображению!
) и хоть и кипят, но черртовски же занятно))
-ШУМ-
Лотелин
mariska
<!--mod1-->
<div class=\'moddiv\'><TABLE cellpadding=\'0\' cellspacing=\'0\' border=\'0\'><TD align=\'middle\' vAlign=\'center\' width=\"1%\" style=\'background-color: #6060ff; color: #ffffff; font-family: Times New Roman, Serif; font-size: 50px; font-weight: bold;\' title=\'Предупреждение\'> i </TD><TD width=\'6px\'>
</TD><TD vAlign=\'middle\'>
<!--emod1-->Учись пользоваться поиском. Переместил.<!--mod2-->
</TD></TABLE></div><!--emod2-->
<!--mod1-->
<div class=\'moddiv\'><TABLE cellpadding=\'0\' cellspacing=\'0\' border=\'0\'><TD align=\'middle\' vAlign=\'center\' width=\"1%\" style=\'background-color: #6060ff; color: #ffffff; font-family: Times New Roman, Serif; font-size: 50px; font-weight: bold;\' title=\'Предупреждение\'> i </TD><TD width=\'6px\'>
</TD><TD vAlign=\'middle\'>
<!--emod1-->Учись пользоваться поиском. Переместил.<!--mod2-->
</TD></TABLE></div><!--emod2-->
Vanilka
Пользователь
Всё равно вы тереть будете эти сообщения, так что выскажусь.
А за что предупреждение? Тему можно было обозвать десятками разных имён. Я вообще не представляю, что бы я вбивала в поиск, если бы мне захотелось найти подобную тему.
Можно было бы вежливо заметить, что такая тема уже существует и указать на неё. И всё.
А за что предупреждение? Тему можно было обозвать десятками разных имён. Я вообще не представляю, что бы я вбивала в поиск, если бы мне захотелось найти подобную тему.
Можно было бы вежливо заметить, что такая тема уже существует и указать на неё. И всё.
[quote name=\'Vanilka\' post=\'413757\' date=\'3.5.2009, 20:20\']Всё равно вы тереть будете эти сообщения, так что выскажусь.
А за что предупреждение? Тему можно было обозвать десятками разных имён. Я вообще не представляю, что бы я вбивала в поиск, если бы мне захотелось найти подобную тему.
Можно было бы вежливо заметить, что такая тема уже существует и указать на неё. И всё.[/quote]
Все нормально, я не воспринимаю это как указание на ошибку, но действительно если это человек новичок и не очень уверенный в себе, это может отбить на какое то время желание открывать новые темы, уж очень вы здесь строгие, по-моему.)
А за что предупреждение? Тему можно было обозвать десятками разных имён. Я вообще не представляю, что бы я вбивала в поиск, если бы мне захотелось найти подобную тему.
Можно было бы вежливо заметить, что такая тема уже существует и указать на неё. И всё.[/quote]
Все нормально, я не воспринимаю это как указание на ошибку, но действительно если это человек новичок и не очень уверенный в себе, это может отбить на какое то время желание открывать новые темы, уж очень вы здесь строгие, по-моему.)
[quote name=\'mariska\' post=\'413761\' date=\'3.5.2009, 21:27\']Все нормально, я не воспринимаю это как указание на ошибку, но действительно если это человек новичок и не очень уверенный в себе, это может отбить на какое то время желание открывать новые темы, уж очень вы здесь строгие, по-моему.)[/quote]
Мариш, ну ведь тебе не отбило, а *скрестила пальцы* (а то кто жеж меня просвесчать будет?) /впрочем, в своем нежелании открывать темы укрепилась/
Мариш, ну ведь тебе не отбило, а *скрестила пальцы* (а то кто жеж меня просвесчать будет?)
/впрочем, в своем нежелании открывать темы укрепилась/
I
Irka
Guest
Vanilka
Синим обозначается просто модераторское замечание, а предупреждение- КРАСНЫМ. Так что рано возмущаешься.
(мое сообщение потом можно потереть)
Синим обозначается просто модераторское замечание, а предупреждение- КРАСНЫМ. Так что рано возмущаешься.
(мое сообщение потом можно потереть)
-ШУМ-
Лотелин
<!--mod1-->
<div class=\'moddiv\'><TABLE cellpadding=\'0\' cellspacing=\'0\' border=\'0\'><TD align=\'middle\' vAlign=\'center\' width=\"1%\" style=\'background-color: #6060ff; color: #ffffff; font-family: Times New Roman, Serif; font-size: 50px; font-weight: bold;\' title=\'Предупреждение\'> i </TD><TD width=\'6px\'>
</TD><TD vAlign=\'middle\'>
<!--emod1-->Так, объясняю для невидящих - предупреждений никто никому не давал, а выделено для того, чтобы обратили внимание, а вот если будем флудить дальше, то они могут вполне реально появиться.
Желающие покатать на меня бочку - в личку, желающие почесать языком - в беседку.<!--mod2-->
</TD></TABLE></div><!--emod2-->
<div class=\'moddiv\'><TABLE cellpadding=\'0\' cellspacing=\'0\' border=\'0\'><TD align=\'middle\' vAlign=\'center\' width=\"1%\" style=\'background-color: #6060ff; color: #ffffff; font-family: Times New Roman, Serif; font-size: 50px; font-weight: bold;\' title=\'Предупреждение\'> i </TD><TD width=\'6px\'>
</TD><TD vAlign=\'middle\'>
<!--emod1-->Так, объясняю для невидящих - предупреждений никто никому не давал, а выделено для того, чтобы обратили внимание, а вот если будем флудить дальше, то они могут вполне реально появиться.
Желающие покатать на меня бочку - в личку, желающие почесать языком - в беседку.<!--mod2-->
</TD></TABLE></div><!--emod2-->